什么是过拟合_什么是过拟合和欠拟合

过拟合：

1、简单理解就是训练样本的得到的输出和期望输出基本一致，但是测试样本输出和测试样本的期望输出相差却很大 。

2、为了得到一致假设而使假设变得过度复杂称为过拟合。想像某种学习算法产生了一个过拟合的分类器，这个分类器能够百分之百的正确分类样本数据（即再拿样本中的文档来给它，它绝对不会分错），但也就为了能够对样本完全正确的分类，使得它的构造如此精细复杂，规则如此严格，以至于任何与样本数据稍有不同的文档它全都认为不属于这个类别！

模型交错和只对模型交错的区别？

在于目标问题的不同。
模型交错是一种训练算法，旨在对大型神经网络进行加速学习，能够显著减少训练时间和代价，并且优化网络性能，从而提高精度。
而只对模型交错是一种指标学习的方法，旨在解决有针对性的数据集优化问题，通过调整指标和损失函数，优先处理最具区分性的样本，从而提高模型的表现。
因此，两种方法在原理和应用场景上有很大的差异。
值得提醒的是，在实际应用中，模型交错和只对模型交错的组合效果往往更好。
尤其是当需要优化分类器的鲁棒性和泛化能力，并且数据集样本分布较为复杂和难以区分时，模型交错和只对模型交错的组合能够有效提高训练效率和表现。

多项式曲线拟合原理？

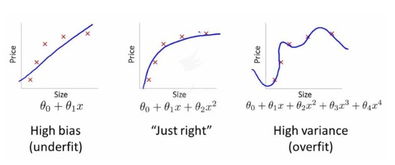
是通过已知数据点的坐标，构建多项式函数来逼近这些数据点，以达到曲线最优拟合的目的。
其中，多项式函数的次数越高，曲线的拟合程度会越高，但是会带来过度拟合的问题。
因此，需要在拟合过程中考虑调整多项式函数阶数，以获得合理的拟合效果。
多项式曲线拟合广泛应用于各种领域，如自然科学、社会科学、经济学等。
在实际应用中，还需要考虑数据的噪声、异常点等因素，以获得更加精确和鲁棒的拟合结果。
同时，也可以使用其他曲线拟合方法，如Bezier曲线、样条曲线等，以满足不同拟合需求。